Separating Axis Theorem
This is a tutorial explaining the Separating Axis Theorem (or the Separating Hyperplane Theorem) as defined by Herman Minkowski. In this document math basics needed to understand the material are reviewed, as well as the Theorem itself, how to implement the Theorem mathematically in two dimensions, creation of a computer program, and test cases proving the Theorem. A completed program is provided at the end of the tutorial. High School algebra is required, as well as an understanding of basic geometry. Previous programming experience is required. Knowledge of JavaScript is helpful.
Math Review
Concepts required to study the Separating Axis Theorem. Algebra and basic Geometry are assumed. This is a review and previous study is helpful.
Vectors
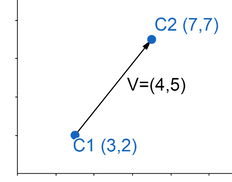
To calculate a vector that points from Coordinate one to coordinate two:
Math Review
Concepts required to study the Separating Axis Theorem. Algebra and basic Geometry are assumed. This is a review and previous study is helpful.
Vectors
To calculate a vector that points from Coordinate one to coordinate two:
- \(\vec{V} = C_2 - C_1\)
Calculate a vector \(\vec{V}\) from \(C_1\) to \(C_2\):
- \(C_1 = (3, 2)\)
- \(C_2 = (7, 7)\)
- \(\vec{V}\hspace{.14cm}= C_2 - C_1\)
- \(\vec{V}\hspace{.14cm}= (7 - 3, 7 - 2)\)
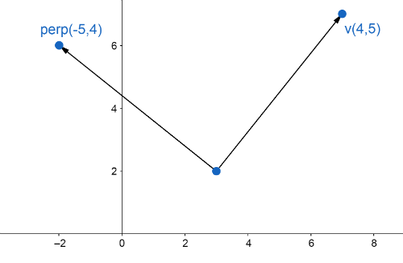
- \(C_2 = (4, 5)\)
- \(\vec{V}\hspace{.23cm}= (4,5)\)
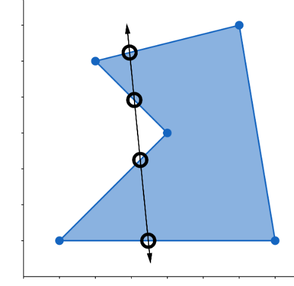
- \(\vec{V}_\perp = (5,4)\)
- \(\vec{V}_\perp = (-5,4)\)
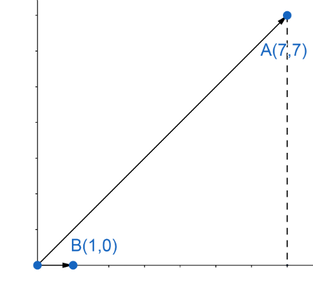
Dot Product
The product of the x component of the first vector and the x component of the second vector summed with the product of the y component of the first vector and the y component of the second vector:
The product of the x component of the first vector and the x component of the second vector summed with the product of the y component of the first vector and the y component of the second vector:
- \(A\centerdot B = A_xB_x + A_yB_y\)
- \(\vec{A}(7,7)\)
- \(\vec{B}(1,0)\)
- \(A\centerdot B = 7(1) + 7(0)\)
- \(A\centerdot B = 7 + 0\)
- \(A\centerdot B = 7\)
Geometry
Convex Polygon
- A polygon that if a line is drawn through the Polygon the line does not intersect the Polygon more then twice.
Concave Polygon
- A polygon that if a line is drawn through the Polygon the line can intersect the polygon more then twice.
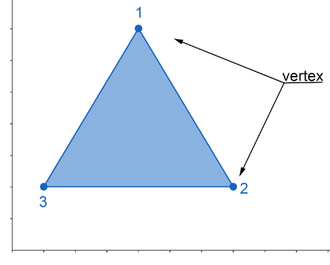
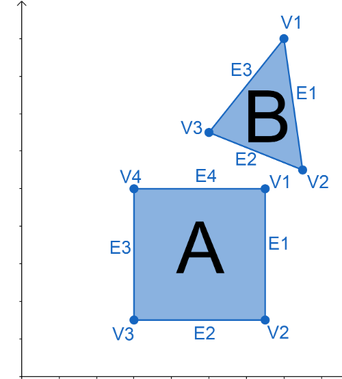
Vertex
A location in Cartesian coordinates that defines where two edges meet in a polygon:
A location in Cartesian coordinates that defines where two edges meet in a polygon:
- \(1 (4,7)\)
- \(2 (7,2)\)
- \(3 (1,2)\)
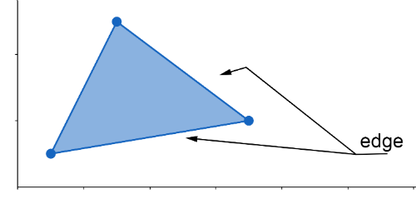
Edge
A line on a polygon that defines the direction and distance to the next vertex.
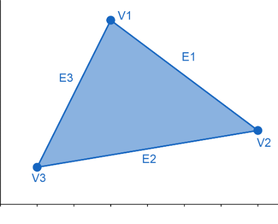
Edges are vectors created from vertices on a polygon in a clockwise motion.
\(E1\) is calculated from \(V1\) and \(V2\):
Theory
The Separating Axis Theorem is a technique for solving convex polygon collision problems. The Theorem postulates if a line can be drawn between two convex (and not concave) polygons the Polyhedra are not colliding. As the Theorem is presented in this tutorial, the Theorem is calculated in two dimensions. The Theorem is a good solution to narrow phase collision detection.
Step 1:
- \(E1 = (4,-3)\)
- \(E2 = (-6,-1)\)
- \(E3 = (2,4)\)
Theory
The Separating Axis Theorem is a technique for solving convex polygon collision problems. The Theorem postulates if a line can be drawn between two convex (and not concave) polygons the Polyhedra are not colliding. As the Theorem is presented in this tutorial, the Theorem is calculated in two dimensions. The Theorem is a good solution to narrow phase collision detection.
Step 1:
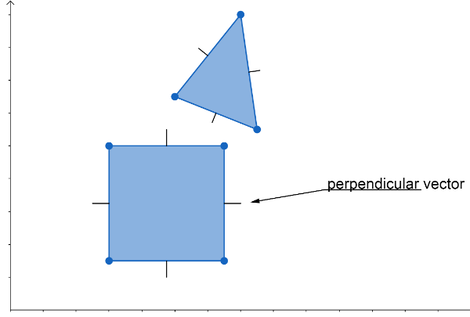
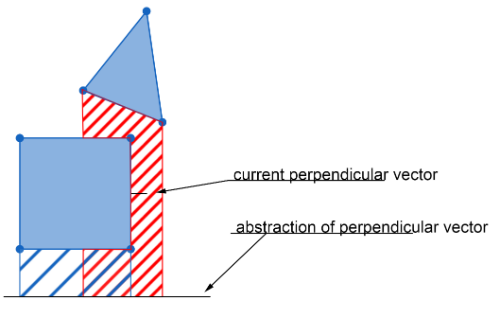
- Calculate perpendicular vectors for all edges.
For each edge on both polygons a perpendicular vector is calculated.
Step 2:
Step 2:
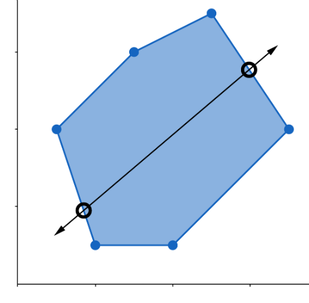
- Project all vertices from the Polyhedra onto each perpendicular vector, one perpendicular vector at a time.
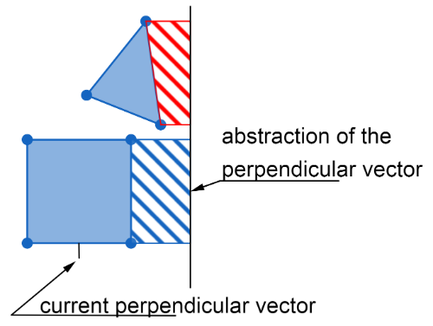
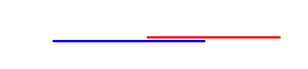
Step 3:
- Check if the projections overlap.
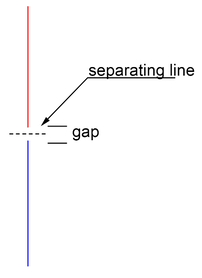
The first projection does not have a gap between the polygons. The image proves that the Polyhedra are not colliding. Another test is necessary because not all perpendicular vectors were tested so it is possible that there could be a projection that can have a separating line drawn between both polygons.
The second projection has a gap. Because a separating line can be drawn between the two polygons, the Theorem concludes that the polygons are not colliding.
Mathematical Application
The Separating Axis Theorem is presented in this section as a mathematical solution.
Step 1:
Mathematical Application
The Separating Axis Theorem is presented in this section as a mathematical solution.
Step 1:
- Create perpendicular vectors for each edge.
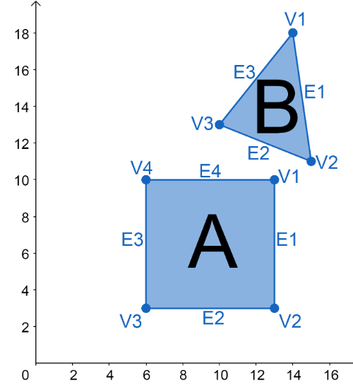
Only calculations for Polygon A Edges one and two will be explained because for this example these are the only two edges that are necessary. It is assumed the polygon details have already been calculated.
Step 2:
Use the Dot Product of each vertex and the perpendicular vector to calculate a one dimensional projection of the Polyhedra. Only the extremities of the Polyhedra will be considered in the interest of space conservation. In practice all vertices should be included in the set. For this calculation \(V1\) and \(V4\) on PolygonA and \(V2\) and \(V3\) on PolygonB were used.
The projections for \(E1_\perp\) are:
- The \(E1\) vector is \((0, -7)\). The perpendicular vector for \(E1\) is \((7, 0)\).
- The \(E2\) vector is \((-7, 0)\). The perpendicular vector for \(E2\) is \((0, -7)\).
Step 2:
Use the Dot Product of each vertex and the perpendicular vector to calculate a one dimensional projection of the Polyhedra. Only the extremities of the Polyhedra will be considered in the interest of space conservation. In practice all vertices should be included in the set. For this calculation \(V1\) and \(V4\) on PolygonA and \(V2\) and \(V3\) on PolygonB were used.
The projections for \(E1_\perp\) are:
- Polygon A:
- \(dot1 = 13(7) + 10(0) = 91\)
- \(dot2 = 6(7) + 10(0) = 42\)
- Polygon B:
- \(dot3 = 15(7) + 11(0) = 105\)
- \(dot4 = 10(7) + 13(0) = 70\)
- \(dot1\) is the result of \(V1\) and \(E1_\perp\)
- \(dot2\) is the result of \(V4\) and \(E1_\perp\)
- \(dot3\) is the result of \(V2\) and \(E1_\perp\)
- \(dot4\) is the result of \(V3\) and \(E1_\perp\)
Normalization of the perpendicular vectors results in projections that are equivalent to the dimensions of the polygon. Normalization is not necessary for the Theorem to calculate correctly.
The projections for \(E2_\perp\) are:
The projections for \(E2_\perp\) are:
- Polygon A:
- \(dot 1 = 13(0) + 10(-7) = -70\)
- \(dot2 = 13(0) + 3(-7) = -21\)
- Polygon B:
- \(dot3 = 14(0) + 18(-7) = -126\)
- \(dot4 = 15(0) + 11(-7) = -77\)
This projection is horizontal and not vertical because the Dot Product projects onto a one dimensional line. The line could be vertical, but the projection does not coincide with the polygon placement. This is of no consequence because the numerical values are being compared, and not the vertical displacement.
Step 3:
Use inequalities to determine if there is a gap between the projections. If there is a gap a separating line can be drawn and the Polyhedra are not colliding.
This is the inequality formula:
Step 3:
Use inequalities to determine if there is a gap between the projections. If there is a gap a separating line can be drawn and the Polyhedra are not colliding.
This is the inequality formula:
|
If the minimal projection value of Polygon A is less then the maximal projection value of Polygon B and the minimal projection value of Polygon A is greater then the minimal projection value of Polygon B or the minimal projection value of Polygon B is less then the maximal projection value of Polygon A and the minimal projection value of Polygon B is greater then the minimal projection value of Polygon A a separating line cannot be drawn.
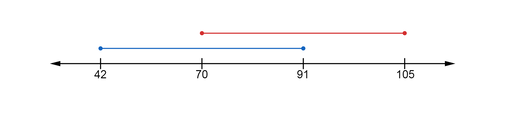
This is the projection for \(E1_\perp\):
This is the projection for \(E1_\perp\):
- \(amin\hspace{.07cm}= 42\)
- \(amax = 91\)
- \(bmin\hspace{.1cm}= 70\)
- \(bmax\hspace{.05cm}= 105\)
\(42 < 105\hspace{.25cm}AND\hspace{.25cm}42 > 70\) |
F |
\(OR\) |
|
\(70 < 91\hspace{.25cm}AND\hspace{.25cm}70 > 42\) |
T |
\(42\) is less then \(105\) but \(42\) is not greater then \(70\). Both statements must be true here because of the logical operand and. This part of the inequality evaluates to false. \(70\) is less then \(91\) and \(70\) is greater then \(42\). Both statements are true here so this part of the inequality evaluates to true. Because of the connective logical operand or only one part of the inequality need evaluate to true for the complete inequality to evaluate to true (2). The complete inequality then evaluates to true. There is an overlap in the projections and no separating line can be drawn. The next perpendicular vector must be checked.
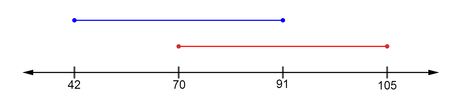
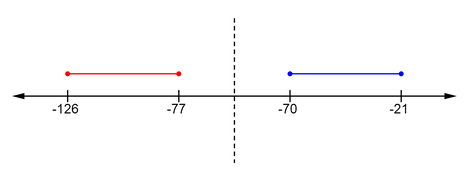
This is the projection for \(E2_\perp\):
This is the projection for \(E2_\perp\):
- \(amin\hspace{.07cm}= -70\)
- \(amax = -21\)
- \(bmin\hspace{.1cm}= -126\)
- \(bmax\hspace{.05cm}= -77\)
\(-70 < -77 \hspace{.25cm} AND \hspace{.25cm} -70 > -126\) |
F |
\(OR\) |
|
\(-126 < -21 \hspace{.25cm} AND \hspace{.25cm} -126 > -70\) |
F |
This inequality evaluates to false. There is a gap in the projections, a separating line can be drawn, the Polyhedra are not colliding. no more checks are necessary. The Theorem is now easily translatable into a program.
Programmatic Application
The Programmatic Application of the Separating Axis Theorem is designed so that all perpendicular vectors are calculated first and pushed onto a stack. The Program then iterates through the stack projecting the Polyhedra onto the perpendicular vectors, checking for a gap which would indicate the ability to draw a separating line between the Polyhedra. The code is presented first with an explanation following.
Declare two functional objects:
Programmatic Application
The Programmatic Application of the Separating Axis Theorem is designed so that all perpendicular vectors are calculated first and pushed onto a stack. The Program then iterates through the stack projecting the Polyhedra onto the perpendicular vectors, checking for a gap which would indicate the ability to draw a separating line between the Polyhedra. The code is presented first with an explanation following.
Declare two functional objects:
function xy(x,y){
this.x = x;
this.y = y;
};
function polygon(vertices,edges){
this.vertex = vertices;
this.edge = edges;
};
|
The xy object, which represents a two dimensional Cartesian point.
The polygon object, which describes a polygon.
Declare a function called “sat” and require two parameters: polygonA and polygonB.
The polygon object, which describes a polygon.
Declare a function called “sat” and require two parameters: polygonA and polygonB.
function sat(polygonA, polygonB){
|
Declare all locally scoped variables:
var perpendicularLine = null;
var dot = 0;
var perpendicularStack = [];
var amin = null;
var amax = null;
var bmin = null;
var bmax = null;
|
The meanings of these variables have already been stated in previous sections.
The perpendicularStack is an array of perpendicularLines.
Step 1:
The perpendicularStack is an array of perpendicularLines.
Step 1:
- Loop through all edges in polygon A:
for(var i = 0; i < polygonA.edge.length; i++){
perpendicularLine = new xy(-polygonA.edge[i].y,
polygonA.edge[i].x);
perpendicularStack.push(perpendicularLine);
}
|
Calculate a perpendicular line.
Push the perpendicular line onto the stack.
Loop through all edges in polygonB.
Push the perpendicular line onto the stack.
Loop through all edges in polygonB.
for(var i = 0; i < polygonB.edge.length; i++){
perpendicularLine = new xy(-polygonB.edge[i].y,
polygonB.edge[i].x);
perpendicularStack.push(perpendicularLine);
}
|
Calculate a perpendicular line.
Push the perpendicular line onto the stack.
Because the possibility exists that not all edges need to be checked, this solution is very wasteful because all edge perpendiculars are calculated in the beginning. This tutorial is meant to explain the Separating Axis Theorem and not proper programming practice.
Loop through each perpendicular line in the stack:
Push the perpendicular line onto the stack.
Because the possibility exists that not all edges need to be checked, this solution is very wasteful because all edge perpendiculars are calculated in the beginning. This tutorial is meant to explain the Separating Axis Theorem and not proper programming practice.
Loop through each perpendicular line in the stack:
for(var i = 0; i < perpendicularStack.length; i++){
amin = null;
amax = null;
bmin = null;
bmax = null;
|
The polygon extent variables need to be reset to null so that future comparisons will be calculated correctly.
Loop through each vertex in PolygonA:
Loop through each vertex in PolygonA:
for(var j = 0; j < polygonA.vertex.length; j++){
|
Step 2:
dot = polygonA.vertex[j].x *
perpendicularStack[i].x +
polygonA.vertex[j].y *
perpendicularStack[i].y;
if(amax === null || dot > amax){
amax = dot;
}
if(amin === null || dot < amin){
amin = dot;
}
}
|
Calculate the Dot Product of the current vertex and the perpendicular line.
Compare the maximal distance of polygonA with the Dot Product. If the Dot Product is greater, set the maximal distance of polygonA to the Dot Product.
Compare the minimal distance of polygonA with the Dot Product. If the Dot Product is less then the minimal distance of polygonA, set the minimal distance of polygonA to the Dot Product.
Note here that a check of null is required to set the initial value. An initial value of zero does not execute properly because the Dot Product can be greater then zero, which means the minimal distance is never saved.
Loop through each vertex in polygonB:
Compare the maximal distance of polygonA with the Dot Product. If the Dot Product is greater, set the maximal distance of polygonA to the Dot Product.
Compare the minimal distance of polygonA with the Dot Product. If the Dot Product is less then the minimal distance of polygonA, set the minimal distance of polygonA to the Dot Product.
Note here that a check of null is required to set the initial value. An initial value of zero does not execute properly because the Dot Product can be greater then zero, which means the minimal distance is never saved.
Loop through each vertex in polygonB:
for(var j = 0; j < polygonB.vertex.length; j++){
|
Repeat Step 2 for polygonB:
dot = polygonB.vertex[j].x *
perpendicularStack[i].x +
polygonB.vertex[j].y *
perpendicularStack[i].y;
if(bmax === null || dot > bmax){
bmax = dot;
}
if(bmin === null || dot < bmin){
bmin = dot;
}
}
|
The process is the same for polygonB except the variables change.
Step 3:
Step 3:
if((amin < bmax && amin > bmin)
||
(bmin < amax && bmin > amin)){
continue;
}
else{
return false;
}
|
Compare the minimal and maximal distances of the Polyhedra to determine the possibility of a separating line.
If the comparison evaluates to true, there is no gap between the projections, continue to the next iteration of the loop until all perpendicular lines are checked for a gap. Otherwise there is a gap or separating line that can possibly be drawn between the Polyhedra. There is no reason to continue, the Polyhedra are not colliding, return false to the calling process:
If the comparison evaluates to true, there is no gap between the projections, continue to the next iteration of the loop until all perpendicular lines are checked for a gap. Otherwise there is a gap or separating line that can possibly be drawn between the Polyhedra. There is no reason to continue, the Polyhedra are not colliding, return false to the calling process:
return true;
|
If all perpendicular lines are checked for a gap and no gap exists, the Polyhedra are colliding. The function returns true to the calling process to indicate this result.
The Separating Axis Theorem Program is compete. What remains is to test the Program to determine if there are any logic errors that require attention.
Tests
Two test cases are presented here. Both test cases involve a square and a triangle. The first test case has no collision between the Polyhedra. The second test case a collision is checked. The program code to determine the objects is also given here, as well as tabled results.
Test One:
The Separating Axis Theorem Program is compete. What remains is to test the Program to determine if there are any logic errors that require attention.
Tests
Two test cases are presented here. Both test cases involve a square and a triangle. The first test case has no collision between the Polyhedra. The second test case a collision is checked. The program code to determine the objects is also given here, as well as tabled results.
Test One:
- PolygonA and PolygonB are not colliding.
- Test One Image.
Key:
Test One Data:
Polygon A:
Programmatic Implementation:
Key:
- V = Vertex
- E = Edge
Test One Data:
Polygon A:
- Vertices:
- \(1: (13,10)\)
- \(2: (13,3)\)
- \(3: (6,3)\)
- \(4: (6,10)\)
- Edges:
- \(1: (0,-7)\)
- \(2: (-7,0)\)
- \(3: (0,7)\)
- \(4: (7,0)\)
- Vertices:
- \(1: (14,18)\)
- \(2: (15,11)\)
- \(3: (10,13)\)
- Edges:
- \(1: (1,-7)\)
- \(2: (-5,2)\)
- \(3: (4,5)\)
Programmatic Implementation:
var polygonAVertices =[
new xy(13,10),
new xy(13,3),
new xy(6,3),
new xy(6,10)]
var polygonAEdges = [
new xy(0,-7),
new xy(-7,0),
new xy(0,7),
new xy(7,0)]
var polygonBVertices = [
new xy(14,18),
new xy(15,11),
new xy(10,13)]
var polygonBEdges = [
new xy(1,-7),
new xy(-5,2),
new xy(4,5)]
var polygonA = new polygon(polygonAVertices,
polygonAEdges)
var polygonB = new polygon(polygonBVertices,
polygonBEdges)
|
Output:
amax |
amin |
bmax |
bmin |
gap |
|
\(1\) |
\(91\) |
\(42\) |
\(105\) |
\(70\) |
No |
\(2\) |
\(-21\) |
\(-70\) |
\(-77\) |
\(-126\) |
Yes |
Because the Program found a gap when projection two occurred, there is no reason to continue to the next perpendicular vector for the next projection calculation. The Polyhedra are not colliding.
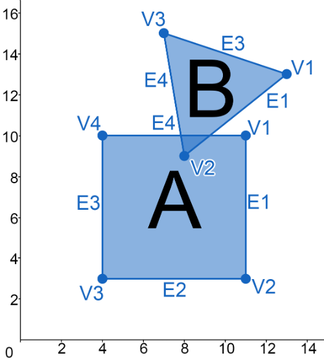
Test Two:
Test Two:
- PolygonA and PolygonB are colliding.
- Test Two Image.
Test Two Data:
Polygon A:
Programmatic Implementation:
Test Two Data:
Polygon A:
- Vertices:
- \(1: (11,10)\)
- \(2: (11,3)\)
- \(3: (4,3)\)
- \(4: (4,10)\)
- Edges:
- \(1: (0,-7)\)
- \(2: (-7,0)\)
- \(3: (0,7)\)
- \(4: (7,0)\)
- Vertices:
- \(1: (13,13)\)
- \(2: (8,9)\)
- \(3: (7,15)\)
- Edges:
- \(1: (-5,-4)\)
- \(2: (-1,6)\)
- \(3: (6,-2)\)
Programmatic Implementation:
var polygonAVertices = [
new xy(11,10),
new xy(11,3),
new xy(4,3),
new xy(4,10)]
var polygonAEdges = [
new xy(0,-7),
new xy(-7,0),
new xy(0,7),
new xy(7,0)]
var polygonBVertices = [
new xy(13,13),
new xy(8,9),
new xy(7,15)]
var polygonBEdges = [
new xy(-5,-4),
new xy(-1,6),
new xy(6,-2)]
var polygonA = new polygon(polygonAVertices,
polygonAEdges)
var polygonB = new polygon(polygonBVertices,
polygonBEdges)
|
Output:
amax |
amin |
bmax |
bmin |
gap |
|
\(1\) |
\(77\) |
\(28\) |
\(91\) |
\(49\) |
No |
\(2\) |
\(-21\) |
\(-70\) |
\(-63\) |
\(-105\) |
No |
\(3\) |
\(-28\) |
\(-77\) |
\(-49\) |
\(-91\) |
No |
\(4\) |
\(70\) |
\(21\) |
\(105\) |
\(63\) |
No |
\(5\) |
\(29\) |
\(-34\) |
\(-13\) |
\(-47\) |
No |
\(6\) |
\(-27\) |
\(-76\) |
\(-57\) |
\(-91\) |
No |
\(7\) |
\(82\) |
\(26\) |
\(104\) |
\(70\) |
No |
The Program checked all Polyhedra projections to conclude that a separating line cannot be drawn between the two polygons. The Polyhedra are colliding.
The logic is correct. The early exit due to the discovery of a separating line is shown in Test One, and the conclusion of a collision in Test Two supports the expectations of the Separating Axis Theorem.
Completed Program
The completed program is presented here. Only the JavaScript code is included as HTML is beyond the scope of this tutorial.
The logic is correct. The early exit due to the discovery of a separating line is shown in Test One, and the conclusion of a collision in Test Two supports the expectations of the Separating Axis Theorem.
Completed Program
The completed program is presented here. Only the JavaScript code is included as HTML is beyond the scope of this tutorial.
function xy(x,y){
this.x = x;
this.y = y;
};
function polygon(vertices, edges){
this.vertex = vertices;
this.edge = edges;
};
//include appropriate test case code.
function sat(polygonA, polygonB){
var perpendicularLine = null;
var dot = 0;
var perpendicularStack = [];
var amin = null;
var amax = null;
var bmin = null;
var bmax = null;
for(var i = 0; i < polygonA.edge.length; i++){
perpendicularLine = new xy(-polygonA.edge[i].y,
polygonA.edge[i].x);
perpendicularStack.push(perpendicularLine);
}
for(var i = 0; i < polygonB.edge.length; i++){
perpendicularLine = new xy(-polygonB.edge[i].y,
polygonB.edge[i].x);
perpendicularStack(perpendicularLine);
}
for(var i = 0; i < perpendicularStack.length; i++){
amin = null;
amax = null;
bmin = null;
bmax = null;
for(var j = 0; j < polygonA.vertex.length; j++){
dot = polygonA.vertex[j].x *
perpenddicularStack[i].x +
polygonA.vertex[j].y *
perpendicularStack[i].y;
if(amax === null || dot < amin){
amax = dot;
}
if(amin === null || dot < amin){
amin = dot;
}
}
for(var j = 0; j < polygonB.vertex.length; j++){
dot = polygonB.vertex[j].x *
perpendicularStack[i].x +
polygonB.vertex[j].y *
perpendicularStack[i].y;
if(bmax === null || dot > bmax){
bmax = dot;
}
if(bmin === null || dot < bmin){
bmin = dot;
}
}
if((amin < bmax && amin > bmin) ||
(bmin < amax && bmin > amin)){
continue;
}
else {
return false;
}
}
return true;
}
|
The Separating Axis Theorem solves convex polygon collision detection problems. The Theorem is simple to understand and implement. This tutorial focused on a JavaScript implementation, but was explained so that translation into another language is not complicated. If the reader is utilizing physics in the design, consider researching the Minimum Translation Vector (MTV). This tutorial did not explain the MTV because the MTV is not part of the Separating Axis Theorem.
Addendum
Below is an HTML document that is downloadable and is the test file that produced the results in the Tests section.
| |||||||
Addendum Two
Programs Used:
Figurations
Vectors:
Footnotes
References
Chong, Kah. Shiu. (2012, August 6). Collision Detection Using the Separating Axis Theorem.
Retrieved from https://gamedevelopment.tutsplus.com/tutorials/collision-detection-using-the-separating-axis-theorem--gamedev-169.
Bittle, William. (2010, January 1). SAT (Separating Axis Theorem).
Retrieved from www.dyn4j.org/2010/01/sat/.
Hyperplane separation theorem. (2018, February 9). In Wikipedia. Retrieved March 27, 2018,
From https://en.wikipedia.org/wiki/Hyperplane_seperation_theorem.
Sevenson, Andrew. (2009, May 24). Separating Axis Theorem (SAT) Explanation.
Retrieved from https://www.sevenson.com.au/actionscript/sat/.
Souto, Nilson. (n.d.). Video Game Physics Tutorial – Part II: Collision Detection For Solid Objects.
Retrieved from https://www.toptal.com/game/video-game-physics-part-ii-collision-detection-for-solid-objects.
Department of Mathematics, Oregon State University(1996.) Dot Products and Projections.
Retrieved from https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/dotprod/dotprod.html.
Dot Product. (2017.). In Math is Fun.
Retrieved March 28th, 2018, from https://www.mathisfun.com/algebra/vectors-dot-product.html.
Nave, R. (n.d.). Basic Vector Operations.
Retrieved from hyperphysics.phy-astr.gsu.edu/hbase/vect.html.
Polygon. (2018, March 28). In Wikipedia.
Retrieved March 28, 2018 from https://en.wikipedia.org/wiki/Polygon.
Addendum Two
Programs Used:
- Code Prettify
- A HTML parser to format a program text on a web page.
- github.com/google/code-prettify
- 2019
- GeoGebra
- An online Math program that allows for graphing Mathematical problems for presentation.
- www.geogebra.org
- 2017
- MathJax
- A HTML parser for formatting Math on a web page.
- www.mathjax.org
- 2019
- Microsoft Windows 7
- An operating system.
- www.microsoft.com
- 2017
- Pixlr
- An online graphics or photo editing program.
- www.pixlr.com
- 2017
Figurations
Vectors:
- Figure 1.
- Figure 2.
- Figure 3.
- Figure 4.
- Figure 5.
- Figure 6.
- Figure 7.
- Figure 8.
- Figure 9.
- Figure 10.
- Figure 11.
- Figure 12.
- Figure 13.
- Figure 14.
- Figure 15.
- Figure 16.
- Figure 17.
- Figure 18.
- Figure 19.
- Figure 20.
Footnotes
- (2) Encyclopedia Britannica Truth table www.britannica.com/topic/truth-table accessed: August 25th, 2018.
References
Chong, Kah. Shiu. (2012, August 6). Collision Detection Using the Separating Axis Theorem.
Retrieved from https://gamedevelopment.tutsplus.com/tutorials/collision-detection-using-the-separating-axis-theorem--gamedev-169.
Bittle, William. (2010, January 1). SAT (Separating Axis Theorem).
Retrieved from www.dyn4j.org/2010/01/sat/.
Hyperplane separation theorem. (2018, February 9). In Wikipedia. Retrieved March 27, 2018,
From https://en.wikipedia.org/wiki/Hyperplane_seperation_theorem.
Sevenson, Andrew. (2009, May 24). Separating Axis Theorem (SAT) Explanation.
Retrieved from https://www.sevenson.com.au/actionscript/sat/.
Souto, Nilson. (n.d.). Video Game Physics Tutorial – Part II: Collision Detection For Solid Objects.
Retrieved from https://www.toptal.com/game/video-game-physics-part-ii-collision-detection-for-solid-objects.
Department of Mathematics, Oregon State University(1996.) Dot Products and Projections.
Retrieved from https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/vcalc/dotprod/dotprod.html.
Dot Product. (2017.). In Math is Fun.
Retrieved March 28th, 2018, from https://www.mathisfun.com/algebra/vectors-dot-product.html.
Nave, R. (n.d.). Basic Vector Operations.
Retrieved from hyperphysics.phy-astr.gsu.edu/hbase/vect.html.
Polygon. (2018, March 28). In Wikipedia.
Retrieved March 28, 2018 from https://en.wikipedia.org/wiki/Polygon.